Intro
Here’s another FiveThirtyEight puzzle from The Riddler. This post is an answer to the Riddler Classic https://fivethirtyeight.com/features/can-you-find-a-matching-pair-of-socks/.
Question
I have 10 pairs of socks in a drawer. Each pair is distinct from another and consists of two matching socks. Alas, I’m negligent when it comes to folding my laundry, and so the socks are not folded into pairs. This morning, fumbling around in the dark, I pull the socks out of the drawer, randomly and one at a time, until I have a matching pair of socks among the ones I’ve removed from the drawer.
On average, how many socks will I pull out of the drawer in order to get my first matching pair?
Answer
With 10 pairs of socks, I can get a pair in 5.68 steps, on average. Here’s how we can simulate the results.
Simulation in R
Load the tidyverse and parallel packages
library(tidyverse)
## -- Attaching packages ------------------- tidyverse 1.3.0 --
## v ggplot2 3.2.1 v purrr 0.3.3
## v tibble 2.1.3 v dplyr 0.8.3
## v tidyr 1.0.0 v stringr 1.4.0
## v readr 1.3.1 v forcats 0.4.0
## -- Conflicts ---------------------- tidyverse_conflicts() --
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()
library(foreach)
##
## Attaching package: 'foreach'
## The following objects are masked from 'package:purrr':
##
## accumulate, when
library(doSNOW)
## Loading required package: iterators
## Loading required package: snowCreate clusters
The way these packages handle parallel computing is to create clusters that can initiate an R script. Each cluster then uses a core to run the code. This is the standard way to initialize and register the number of clusters.
cl<-makeCluster(3) # change the 3 to the number of CPU cores you want to use
registerDoSNOW(cl)Foreach loop
Just like the other Riddler, I’m going to write a foreach-loop. Here’s a link about the basics of foreach https://www.r-bloggers.com/parallel-r-loops-for-windows-and-linux/.
foreach usually results in a list, but we can get it to output a vector by adding .combine = 'c'. %dopar% is the parallel version of %do%, and the only thing different is that it requires preregistered clusters.
Every element of the many_runs vector will be the number of socks required to get a match.
# Initialize starting variables
socks = 1:10
number_of_matches = 1e4
# Run simulations
many_runs = foreach(1:number_of_matches, .combine = 'c') %dopar% {
# Two sock elements because there are pairs in the drawer
drawer = c(socks,socks)
# Start empty handed
pull_sock = NULL
socks_in_hand = NULL
# Run the while loop until there's one duplicate and length(unique) is shorter than length
while ( length(unique(socks_in_hand)) == length(socks_in_hand) ) {
# sample and do not replace
pull_sock = sample(drawer, 1, replace = FALSE)
# put the sock in hand
socks_in_hand = c(socks_in_hand, pull_sock)
# remove the sock from the drawer
# The match returns the first matching index of the pull sock in the drawer
# - removes that index
# So the new drawer is the old drawer without the pulled sock
drawer = drawer[-match(pull_sock, drawer)]
}
# send this number to the many_runs vector
length(socks_in_hand)
}Stop clusters
Now we’ll close our clusters. Eventually, the clusters close after some period of inactivity, but it’s best practice to stop them in the code.
stopCluster(cl)Results
kableExtra::kable(tibble(Mean = mean(many_runs)))| Mean |
|---|
| 5.6981 |
Histogram
hist(many_runs)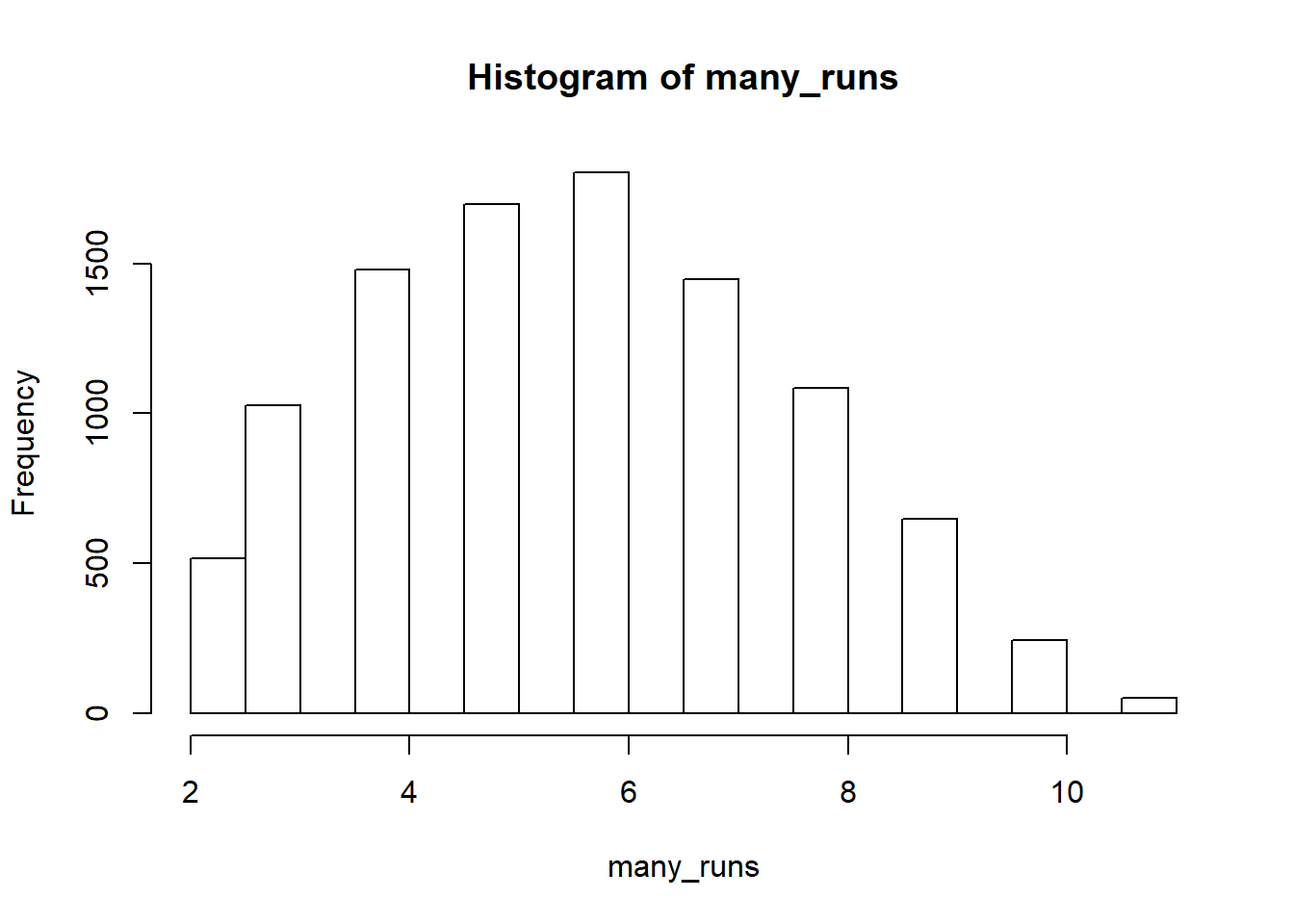
Frequency Table
kableExtra::kable(t(table(many_runs)))| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|
| 517 | 1027 | 1480 | 1699 | 1802 | 1448 | 1085 | 648 | 243 | 51 |
Percentage Table
percent_tibble = tibble(`Socks grabbed: ` = names(table(many_runs)),
`Percentage: ` = paste0(round(table(many_runs)/number_of_matches*100,1),"%"))
kableExtra::kable(t(percent_tibble))| Socks grabbed: | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Percentage: | 5.2% | 10.3% | 14.8% | 17% | 18% | 14.5% | 10.8% | 6.5% | 2.4% | 0.5% |